Ein Innenwinkel ist ein Winkel innerhalb einer Form
Ein weiteres Beispiel:
Dreiecke
Die Innenwinkel eines Dreiecks addieren sich zu 180°
Versuchen wir ein dreieck: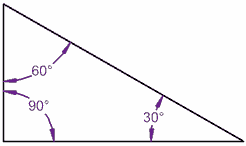
90° + 60° + 30° = 180°
Es funktioniert für dieses Dreieck
Jetzt eine Linie um 10°kippen: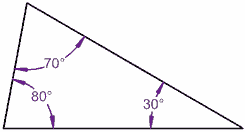
80° + 70° + 30° = 180°
Es funktioniert immer noch!,
Ein Winkel stieg um 10°,
und der andere um 10°
Vierecke (Quadrate usw.)
(Ein Viereck hat 4 gerade Seiten)
Die Innenwinkel eines Vierecks summieren sich auf 360°
, da sich in einem Quadrat 2 Dreiecke befinden …
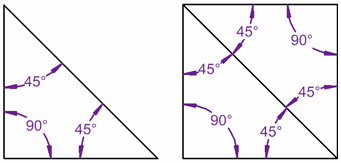
Die Innenwinkel in einem Dreieck summieren sich auf 180° …
… und für das Quadrat addieren sie sich zu 360° …
… weil das Quadrat aus zwei Dreiecken gemacht werden kann!,
Fünfeck
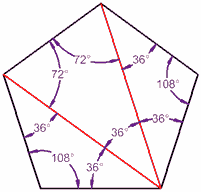
Ein Fünfeck hat 5 Seiten und kann aus drei Dreiecken bestehen, damit Sie wissen, was …
…,hen es regelmäßig ist (alle Winkel gleich), dann ist jeder Winkel 540° / 5 = 108°
(Übung: Stellen Sie sicher, dass sich jedes Dreieck hier zu 180° addiert, und überprüfen Sie, ob sich die Innenwinkel des Fünfecks zu 540°addieren)
Die Innenwinkel eines Fünfecks addieren sich zu 540°
Die allgemeine Regel
Jedes Mal, wenn wir eine Seite hinzufügen (Dreieck zu Viereck, Viereck zu Fünfeck usw.), fügen wir die Summe:
Die allgemeine Regel lautet also:
Summe der Innenwinkel = (n−2) × 180°
Jeder Winkel (eines regulären Polygons) = (n−2) × 180° / n
Vielleicht hilft ein Beispiel:


Schreibe einen Kommentar