Sezione conica: una sezione (o fetta) attraverso un cono.

Cones

Circle
straight through
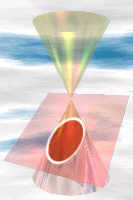
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle
So all those curves are related!
Focus!,

Le curve possono anche essere definite usando una linea retta e un punto (chiamato directrix e focus).
Quando misuriamo la distanza:
- dalla messa a fuoco a un punto della curva, e
- perpendicolarmente dalla direttrice a quel punto
le due distanze saranno sempre lo stesso rapporto.
- Per un’ellisse, il rapporto è inferiore a 1
- Per una parabola, il rapporto è 1, quindi le due distanze sono uguali.,
- Per un iperbole, il rapporto è superiore a 1
Eccentricità
il rapporto di cui sopra è chiamato il “eccentricità”, quindi possiamo dire che ogni conica è:
“tutti i punti la cui distanza per la messa a fuoco è uguale
per l’eccentricità volte la distanza dalla direttrice”
Per:
- 0 < eccentricità < 1 si ottiene un’ellisse,
- eccentricità = 1 parabola, e
- eccentricità > 1 una iperbole.,
Un cerchio ha un’eccentricità pari a zero, quindi l’eccentricità ci mostra quanto sia “non circolare” la curva. Più grande è l’eccentricità, meno è curva.
Latus Rectum

Il latus rectum (no, non è una parola maleducata!) corre parallelo alla direttrice e passa attraverso lo stato attivo. La sua lunghezza:
- In una parabola, è quattro volte la lunghezza focale
- In un cerchio, è il diametro
- In un’ellisse, è 2b2 / a (dove a e b sono la metà del diametro maggiore e minore).,
Ecco l’asse maggiore e l’asse minore di un’ellisse.
C’è un focus e una direttrice su ciascun lato (cioè una coppia di essi).,
Equazioni
Quando posto come questo su un grafico x-y, l’equazione di un’ellisse è:
x2a2 + y2b2 = 1
Il caso particolare di un cerchio di raggio=a=b):
x2a2 + y2a2 = 1
E per un iperbole è:
x2a2 − y2b2 = 1
Equazione Generale
Si può fare un’equazione che copre tutte queste curve.,
Poiché sono curve piane (anche se tagliate fuori dal solido) dobbiamo solo avere a che fare con le coordinate cartesiane (“x” e “y”).
Ma queste non sono linee rette, quindi solo “x” e “y” non lo faranno … dobbiamo passare al livello successivo e avere:
- x2 e y2,
- e anche x (senza y), y (senza x),
- x e y insieme (xy)
- e un termine costante.
Lì, che dovrebbe farlo!
E ognuno ha bisogno di un fattore (A,B,C ecc.) …,
Quindi l’equazione generale che copre tutte le sezioni coniche è:
![]()
E da quell’equazione possiamo creare equazioni per il cerchio, l’ellisse, la parabola e l’iperbole.




Lascia un commento