Kjeglesnitt

Ikpsoniske Avsnittet: en del (eller slice) gjennom en membran.

Cones

Circle
straight through

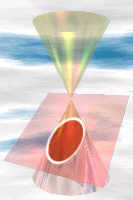
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle

So all those curves are related!

Focus!,

kurvene kan også defineres ved hjelp av en rett linje og et punkt (kalt styrelinje og fokus).

Når vi måler avstand:

• fra fokus til et punkt på kurven, og
• loddrett fra styrelinje til at punkt

de to avstander vil alltid være det samme forholdet.

• For en ellipse, forholdet er mindre enn 1
• For en parabel, forholdet er 1, så de to avstandene er like.,
• For en hyperbel, forholdet er større enn 1

Eksentrisitet

Det forholdet som er beskrevet ovenfor er kalt «eksentrisitet», så kan vi si at alle ikpsoniske delen er:

For:

• 0 < eksentrisitet < 1 får vi en ellipse,
• eksentrisitet = 1 en parabel, og
• eksentrisitet > 1 en hyperbel.,

En sirkel har en eksentrisitet på null, så eksentrisitet viser oss hvordan «fn-sirkulære» kurven er. Jo større eksentrisitet, jo mindre buet det er.

Latus Rectum

latus rectum (nei, det er ikke ett uhøflig ord!) går parallelt med den styrelinje og går gjennom fokus. Lengde:

• I en parabel, er fire ganger brennvidden
• I en sirkel er diameteren
• I en ellipse, er 2b2/a (der a og b er den ene halvdelen av større og mindre diameter).,

Her er den store aksen og mindre aksen av en ellipse.

Det er et fokus og styrelinje på hver side (dvs et par av dem).,

Ligninger

Når den plasseres som dette på et x-y-diagram, formelen for en ellipse er:

x2a2 + y2b2 = 1

Det spesielle tilfellet av en sirkel (hvor radius=a=b):

x2a2 + y2a2 = 1

Og for en hyperbel det er:

x2a2 − y2b2 = 1

Generelle Ligningen

Vi kan lage en ligning som dekker alle disse kurvene.,

Fordi de er plane kurver (selv om kutt ut av solid) vi har kun avtale med Kartesiske («x» og «y») Koordinater.

Men disse er ikke rette linjer, så det er bare å «x» og «y» ikke vil gjøre … vi trenger ikke å gå til neste nivå, og har:

• x2 og y2,
• og også x (uten y), y (uten x)
• x-og y-sammen (xy)
• og en konstant sikt.

Det, som bør gjøre det!

hver Og en trenger en faktor (A,B,C osv) …,

Så den generelle ligningen som dekker alle kjeglesnitt er:

Og fra denne ligningen kan vi lage ligninger for sirkel, ellipse, parabel og hyperbel.