Kegelsneden

kegelsneden: een doorsnede (of schijfje) door een kegel.

Cones

Circle
straight through

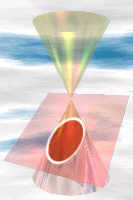
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle

So all those curves are related!

Focus!,

De curves kunnen ook worden gedefinieerd met behulp van een rechte lijn en een punt (directrix en focus genoemd).

wanneer we de afstand meten:

• van het scherpstelpunt naar een punt op de curve, en
• loodrecht van de directrix naar dat punt

zullen de twee afstanden altijd dezelfde verhouding zijn.

• voor een ellips is de verhouding kleiner dan 1
• voor een parabool is de verhouding 1, dus de twee afstanden zijn gelijk.,
• Voor een hyperbool, de verhouding groter is dan 1

Excentriciteit

Die ratio boven is genoemd de “excentriciteit”, dus we kunnen zeggen dat een kegelsnede is:

Voor:

• 0 < excentriciteit < 1 krijgen we een ellips,
• excentriciteit = 1 een parabool, en
• excentriciteit > 1 een hyperbool.,

een cirkel heeft een excentriciteit van nul, dus de excentriciteit toont ons hoe “On-cirkelvormig” de kromme is. Hoe groter de excentriciteit, hoe minder gebogen het is.

Latus Rectum

Het latus rectum (Nee, Het is geen grof woord!) loopt parallel aan de directrix en gaat door de focus. De lengte:

• in een parabool, is vier keer de brandpuntsafstand
• In een cirkel, is de diameter
• In een ellips, is 2b2 / a (waarbij a en b de helft van de grote en kleine diameter zijn).,

Hier is de hoofdas en de kleine as van een ellips.

Er is een focus en directrix aan elke kant (dat wil zeggen een paar van hen).,

Vergelijkingen

Wanneer geplaatst, zoals deze op een x-y grafiek, is de vergelijking voor een ellips is:

x2a2 + y2b2 = 1

Het speciale geval van een cirkel (met radius=a=b):

x2a2 + y2a2 = 1

En voor een hyperbool is:

x2a2 − y2b2 = 1

Algemene Vergelijking

Wij kunnen een vergelijking die betrekking heeft op al deze curven.,

omdat het vlakke krommen zijn (ook al zijn ze uit de vaste stof gesneden) hebben we alleen te maken met Cartesische (“x” en “y”) coördinaten.

maar dit zijn geen rechte lijnen, dus alleen “x” en ” y ” zijn niet voldoende … we moeten naar het volgende niveau, en hebben:

• x2 en y2,
• en ook x (zonder y), y (zonder x),
• x en y samen (xy)
• en een constante term.

daar, dat zou het moeten doen!

en elk heeft een factor nodig (A,B,C enz.)…,

de algemene vergelijking die alle kegelsneden dekt is:

en uit die vergelijking kunnen we vergelijkingen maken voor de cirkel, ellips, parabool en hyperbool.