sekcja stożkowa: sekcja (lub przecięcie) przez stożek.

Cones

Circle
straight through
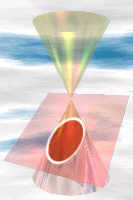
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle
So all those curves are related!
Focus!,
krzywe mogą być również zdefiniowane za pomocą linii prostej i punktu (zwanego directrix i focus).
Kiedy mierzymy odległość:
- od punktu skupienia do punktu na krzywej i
- prostopadle od punktu skupienia do tego punktu
obie odległości będą zawsze takie same.
- dla elipsy stosunek jest mniejszy niż 1
- dla paraboli stosunek jest 1, więc dwie odległości są równe.,
- dla hiperboli stosunek jest większy niż 1
ekscentryczność
powyższy stosunek nazywa się „ekscentrycznością”, więc możemy powiedzieć, że dowolny odcinek stożkowy to:
„wszystkie punkty, których odległość do ogniska jest równa
do ekscentryczności razy odległość do directrix”
dla:
- 0 < ekscentryczność < 1 otrzymujemy elipsę,
- ekscentryczność = 1 A parabola, i
- ekscentryczność > 1 A hiperbola.,
okrąg ma ekscentryczność zerową, więc ekscentryczność pokazuje nam, jak „niekolisty” jest krzywa. Im większa mimośrodowość, tym mniej zakrzywiona.
Latus Rectum

latus rectum (nie, to nie jest niegrzeczne słowo!) biegnie równolegle do directrix i przechodzi przez fokus. Jego długość:
- w paraboli, jest czterokrotna ogniskowa
- w okręgu, jest średnicą
- w elipsie, wynosi 2b2 / a (gdzie a i b są połową średnicy głównej i małej).,
oto główna oś i mała oś elipsy.
po każdej stronie znajduje się focus i directrix (czyli para).,
równania
Po umieszczeniu w ten sposób na wykresie X-y równanie elipsy wynosi:
x2a2 + y2b2 = 1
specjalny przypadek okręgu (gdzie promień=a=b):
x2a2 + y2a2 = 1
a dla hiperboli jest to:
x2a2 − y2b2 = 1
równanie ogólne
możemy utworzyć równanie obejmujące wszystkie te krzywe.,
ponieważ są to krzywe płaszczyznowe (choć wycięte z bryły), mamy do czynienia jedynie ze współrzędnymi Kartezjańskimi („x” i „y”).
ale nie są to linie proste, więc tylko „x” i „y” nie wystarczą … musimy przejść do następnego poziomu i mieć:
- x2 i y2,
- a także x (bez y), y (bez x),
- X i Y razem (xy)
- oraz stały termin.
To powinno wystarczyć!
i każdy z nich potrzebuje czynnika (A,B, C itp.)…,
tak więc ogólne równanie obejmujące wszystkie sekcje stożkowe to:
![]()
i z tego równania możemy tworzyć równania dla okręgu, elipsy, paraboli i hiperboli.





Dodaj komentarz