secção Cónica: secção (ou fatia) através de um cone.sabia que ao levar diferentes fatias através de um cone, pode criar um círculo, uma elipse, uma parábola ou uma hipérbole?,

Cones

Circle
straight through
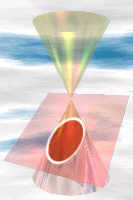
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle
So all those curves are related!
Focus!,
As curvas também podem ser definidas usando uma linha reta e um ponto (o chamado directrix e foco).
quando medimos a distância:
- do foco a um ponto na curva, e
- perpendicularmente da directriz a esse ponto
as duas distâncias serão sempre a mesma razão.
- para uma elipse, a razão é inferior a 1
- Para uma parábola, a razão é 1, de modo que as duas distâncias são iguais.,
- Para uma hipérbole, a proporção é maior do que 1
Excentricidade
Essa relação acima é chamado de a “excentricidade”, portanto, podemos dizer que qualquer cônica de seção é:
“todos os pontos cuja distância ao foco é igual
para a excentricidade vezes a distância para a directrix”
Para:
- 0 < excentricidade < 1 temos uma elipse,
- excentricidade = 1 uma parábola, e
- excentricidade > 1 uma hipérbole.,
um círculo tem uma excentricidade de zero, por isso a excentricidade mostra-nos como a curva é “não circular”. Quanto maior a excentricidade, menos curva é.
Latus Rectum
O latus rectum (não, não é um palavrão!) corre paralelamente à directriz e passa através do foco. Seu tamanho:
- Em uma parábola, é de quatro vezes o comprimento focal
- Em um círculo, é o diâmetro
- Em uma elipse, é 2b2/a (onde a e b são a metade do maior e menor diâmetro).,
Aqui está o eixo principal e o eixo menor de uma elipse.
Há um foco e directriz em cada lado (ou seja, um par deles).,
Equações
Quando colocado como este em um gráfico x-y, a equação de uma elipse é:
x2a2 + y2b2 = 1
O caso especial de um círculo com raio=a=b):
x2a2 + y2a2 = 1
E para uma hipérbole é:
x2a2 − y2b2 = 1
Equação Geral
Nós podemos fazer uma equação que engloba todas essas curvas.,
porque eles são curvas planas (embora cortadas do sólido) nós só temos que lidar com coordenadas cartesianas (“x” e “y”).
mas estas não são linhas retas, por isso apenas “x” e “y” não serve … precisamos ir para o próximo nível, e tem:
- x2 e y2
- e também x (sem y), y (sem o x),
- x e y juntas (xy)
- e um termo constante. isso deve bastar!
e cada um necessita de um factor (a,B,C etc.)…,
assim, a equação geral que cobre todas as seções cónicas é:
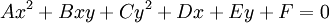
e a partir dessa equação podemos criar equações para o círculo, elipse, parábola e hipérbole.






Deixe uma resposta