secțiune conică: o secțiune (sau felie) printr-un con.știați că luând diferite felii printr-un con puteți crea un cerc, o elipsă, o parabolă sau o hiperbolă?,

Cones

Circle
straight through
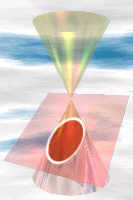
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle
So all those curves are related!
Focus!,
curbe, de asemenea, pot fi definite folosind o linie dreaptă și un punct (numit pe directoare și să se concentreze).când măsurăm distanța:
- de la focalizare la un punct de pe curbă și
- perpendicular de la directrix la acel punct
cele două distanțe vor fi întotdeauna același raport.pentru o elipsă, raportul este mai mic de 1
Excentricitate
Care raportul de mai sus este numit „excentricitate”, deci putem spune că orice secțiune conică este:
„toate punctele ale căror distanta de la accentul este egal cu
pentru excentricitatea de ori distanța de la directoarea”
Pentru:
- 0 < excentricitate < 1 vom obține o elipsă,
- excentricitate = 1 o parabolă, și
- excentricitate > 1 o hiperbolă.,
un cerc are o excentricitate de zero, astfel încât excentricitatea ne arată cât de” ne-circulară ” este curba. Cu cât excentricitatea este mai mare, cu atât este mai puțin curbată.
Latus Rectum
latus rectum (nu, nu este un cuvant nepoliticos!) rulează paralel cu directtrix și trece prin focalizare. Lungimea sa:
- Într-o parabolă, este de patru ori distanța focală
- Într-un cerc, este diametrul
- Într-o elipsă, este 2b2/a (unde a și b sunt de o jumătate de majore și minore diametru).,
Iată axa majoră și axa minoră a unei elipse. există o focalizare și o directrix pe fiecare parte (adică o pereche de ele).,
Diferentiale
atunci Când sunt plasate astfel pe un x-y grafic, ecuația unei elipse este:
x2a2 + y2b2 = 1
caz special de cerc (în cazul în care raza=a=b):
x2a2 + y2a2 = 1
Și pentru o hiperbolă este:
x2a2 − y2b2 = 1
Ecuația Generală
putem face o ecuație care acoperă toate aceste curbe.,
deoarece sunt curbe plane (chiar dacă sunt decupate din solid), trebuie să avem de-a face doar cu coordonatele carteziene („x” și „y”). dar acestea nu sunt linii drepte, deci doar „x” și „y” nu vor face … trebuie să trecem la nivelul următor și să avem:
- x2 și y2,
- și, de asemenea, x (fără y), y (fără x),
- x și Y împreună (xy)
- și un termen constant.
acolo, asta ar trebui să o facă!
și fiecare are nevoie de un factor (A,B,C etc) …,
Deci ecuația generală care acoperă toate secțiunile conice este:
![]()
Și din această ecuație putem crea ecuații pentru cerc, elipsă, parabolă și hiperbolă.






Lasă un răspuns