SPSS-Korrelationsanalyse-Tutorial

Siehe auch Pearson-Korrelationen-Schnelle Einführung.

• Korrelationstest – Was ist das?
• Nullhypothese
• Annahmen
• Korrelationstest in SPSS
• Berichterstattung

Korrelationstest-Was ist das?

Eine (Pearson -) Korrelation ist eine Zahl zwischen -1 und +1, die angibt, inwieweit 2 quantitative Variablen linear verwandt sind. Es wird am besten verstanden, wenn man sich einige Scatterplots ansieht.,

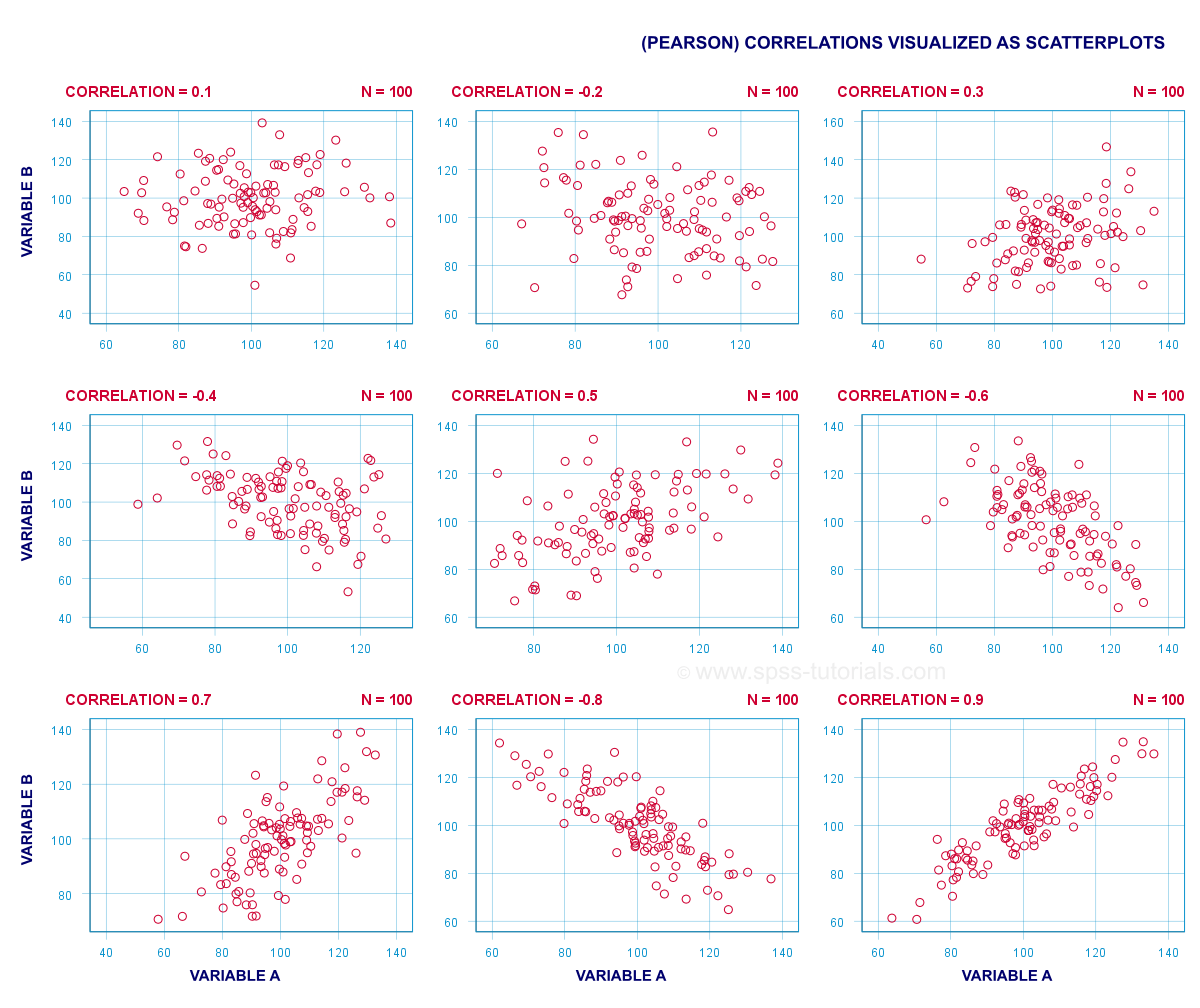
Kurz gesagt,

• Eine Korrelation von -1 zeigt eine perfekte lineare absteigende Beziehung an: Höhere Werte für eine Variable implizieren niedrigere Werte für die andere Variable.
• Eine Korrelation von 0 bedeutet, dass es keine lineare Beziehung zwischen 2 Variablen gibt. Es kann jedoch dennoch eine (starke) nichtlineare Beziehung geben.
• Eine Korrelation von 1 zeigt eine perfekte aufsteigende lineare Beziehung an: Höhere Werte für eine Variable sind mit höheren Werten für die andere Variable verbunden.,

Nullhypothese

Ein Korrelationstest (normalerweise) testet die Nullhypothese, dass die Populationskorrelation Null ist.Daten enthalten oft nur eine Stichprobe aus einer (viel) größeren Population: Ich habe 100 Kunden befragt (Stichprobe), aber ich interessiere mich wirklich für alle meine 100.000 Kunden (Bevölkerung). Die Ergebnisse der Stichprobe unterscheiden sich typischerweise etwas von den Ergebnissen der Bevölkerung. Das Finden einer Korrelation ungleich Null in meiner Stichprobe beweist also nicht, dass 2 Variablen in meiner gesamten Population korreliert sind; Wenn die Populationskorrelation wirklich Null ist, kann ich leicht eine kleine Korrelation in meiner Stichprobe finden., Es ist jedoch sehr unwahrscheinlich, in diesem Fall eine starke Korrelation zu finden, und legt nahe, dass meine Populationskorrelation schließlich nicht Null war.

Korrelationstest-Annahmen

Die Berechnung und Interpretation von Korrelationskoeffizienten selbst erfordert keine Annahmen. Der statistische Signifikanztest für Korrelationen setzt jedoch

• unabhängige Beobachtungen voraus;
• Normalität: Unsere 2 Variablen müssen einer bivariaten Normalverteilung in unserer Population folgen. Diese Annahme ist für Stichprobengrößen von N = 25 oder mehr nicht erforderlich.,Bei vernünftigen Stichprobengrößen stellt der zentrale Grenzwertsatz sicher, dass die Stichprobenverteilung normal ist.

SPSS-Quick Data Check

Lassen Sie uns jetzt einige Korrelationstests in SPSS durchführen. Wir werden Jugendliche benutzen.sav, eine Datendatei, die psychologische Testdaten zu 128 Kindern zwischen 12 und 14 Jahren enthält. Ein Teil seiner Variablenansicht ist unten dargestellt.

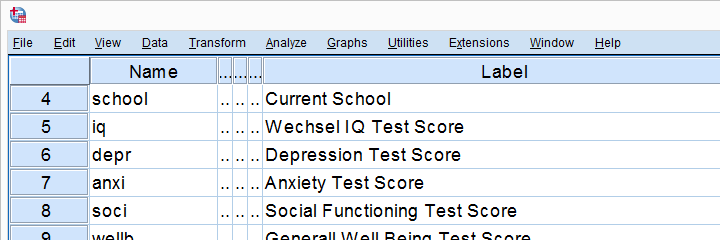
Bevor wir nun Korrelationen ausführen, stellen wir zunächst sicher, dass unsere Daten überhaupt plausibel sind., Da alle 5 Variablen metrisch sind, überprüfen wir ihre Histogramme schnell, indem wir die folgende Syntax ausführen.

Histogrammausgabe

Unsere Histogramme sagen uns viel: Unsere Variablen haben zwischen 5 und 10 fehlende Werte. Ihre Mittel sind nahe bei 100 mit Standardabweichungen um 15 -was gut ist, weil diese Tests so kalibriert wurden. Eine Sache stört mich jedoch, und es ist unten gezeigt.,

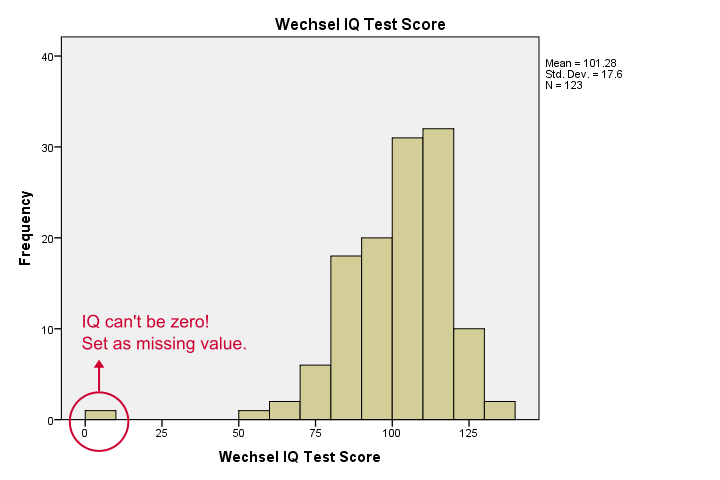
Es scheint, als hätte jemand bei einigen Tests Null erzielt-was überhaupt nicht plausibel ist. Wenn wir dies ignorieren, werden unsere Korrelationen stark voreingenommen sein. Lassen Sie uns unsere Fälle sortieren, sehen, was los ist und einige fehlende Werte festlegen, bevor Sie fortfahren.

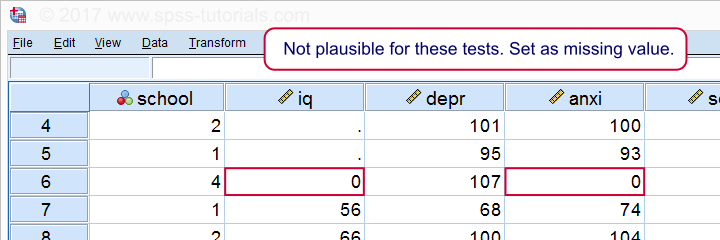
Wenn wir jetzt unsere Histogramme erneut ausführen, werden wir sehen, dass alle Verteilungen plausibel aussehen., Erst jetzt sollten wir mit den tatsächlichen Korrelationen fortfahren.

Ausführen eines Korrelationstests in SPSS

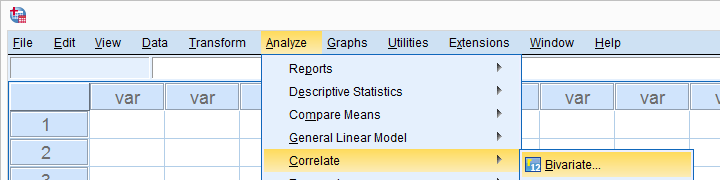
Navigieren wir zuerst zu Analyze Correlate Bivariate wie unten gezeigt.

Verschieben Sie alle relevanten Variablen in das Feld Variablen. Sie möchten hier wahrscheinlich nichts anderes ändern.

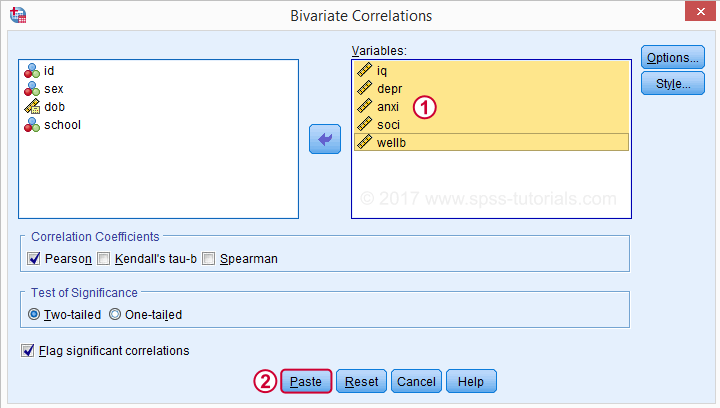
Wenn Sie auf Einfügen klicken, wird die folgende Syntax angezeigt. Lass es uns laufen.

SPSS-KORRELATIONEN Syntax

Korrelationsausgabe

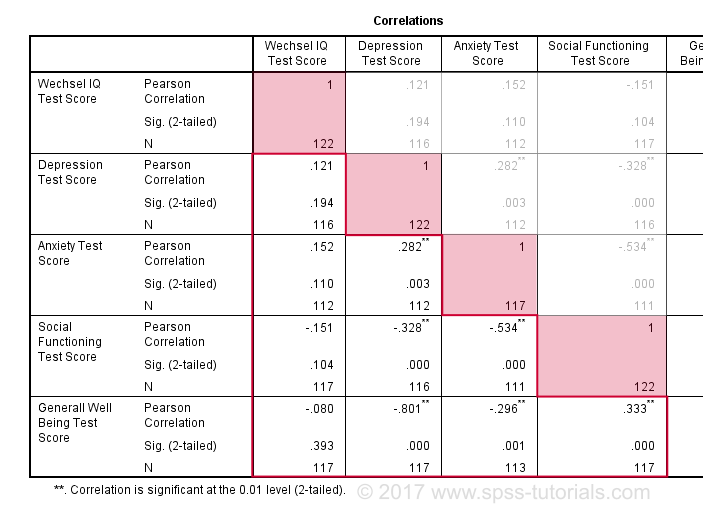
Standardmäßig erstellt SPSS immer eine vollständige Korrelationsmatrix. Jede Korrelation erscheint zweimal: über und unter der Hauptdiagonale. Die Korrelationen auf der Hauptdiagonale sind die Korrelationen zwischen jeder Variablen und sich selbst-weshalb sie alle 1 und überhaupt nicht interessant sind. Die 10 Korrelationen unterhalb der Diagonale sind das, was wir brauchen., Als Faustregel gilt, dass eine Korrelation statistisch signifikant ist, wenn ihre “ Sig. (2-tailed)“ < 0.05.Schauen wir uns nun unsere Ergebnisse genau an: Die stärkste Korrelation besteht zwischen Depression und allgemeinem Wohlbefinden : r = -0.801. Es basiert auf N = 117 Kindern und seiner 2-tailed Bedeutung, p = 0,000. Dies bedeutet, dass eine Wahrscheinlichkeit von 0,000 besteht, diese Stichprobenkorrelation-oder eine größere – zu finden, wenn die tatsächliche Populationskorrelation Null ist.
Beachten Sie, dass IQ nicht mit irgendetwas korrelieren. Seine stärkste Korrelation ist 0.152 mit Angst, aber p = 0.,11 es unterscheidet sich also statistisch nicht signifikant von Null. Das heißt, es besteht eine Chance von 0.11, sie zu finden, wenn die Populationskorrelation Null ist. Diese Korrelation ist zu klein, um die Nullhypothese abzulehnen.
Wie so zeigen unsere 10 Korrelationen an, inwieweit jedes Variablenpaar linear verwandt ist. Beachten Sie abschließend, dass jede Korrelation auf einem etwas anderen N berechnet wird-im Bereich von 111 bis 117. Dies liegt daran, dass SPSS das paarweise Löschen fehlender Werte standardmäßig für Korrelationen verwendet.,

Scatterplots

Streng genommen sollten wir auch alle Scatterplots unter unseren Variablen untersuchen. Schließlich könnten Variablen, die nicht korrelieren, immer noch nicht linear verwandt sein. Aber für mehr als 5 oder 6 Variablen explodiert die Anzahl der möglichen Scatterplots, so dass wir sie oft überspringen. Siehe jedoch SPSS-Create All Scatterplots Werkzeug.
Die Syntax unten erstellt nur ein Scatterplot, nur um eine Vorstellung davon zu bekommen, wie unsere Beziehung aussieht. Das Ergebnis zeigt jedoch nichts Unerwartetes.

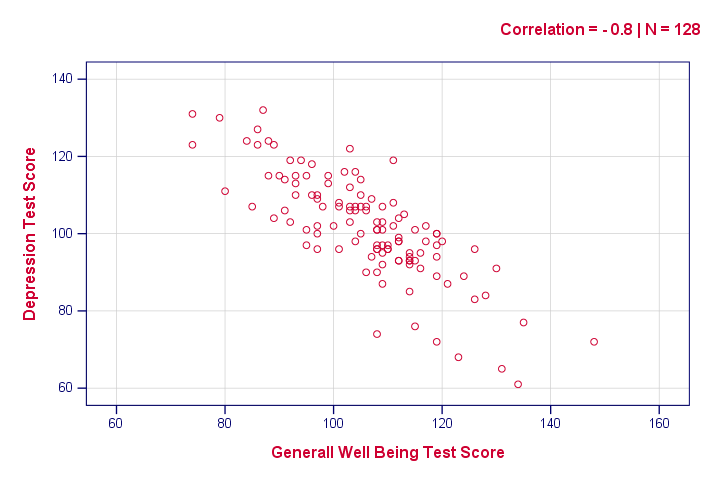
Meldung eines Korrelationstests

Die folgende Abbildung zeigt das grundlegendste Format, das von der APA für die Meldung von Korrelationen empfohlen wird. Stellen Sie sicher, dass die Tabelle angibt, welche Korrelationen bei p < 0.05 und möglicherweise p < 0.01 statistisch signifikant sind. Siehe auch SPSS Korrelationen im APA-Format.

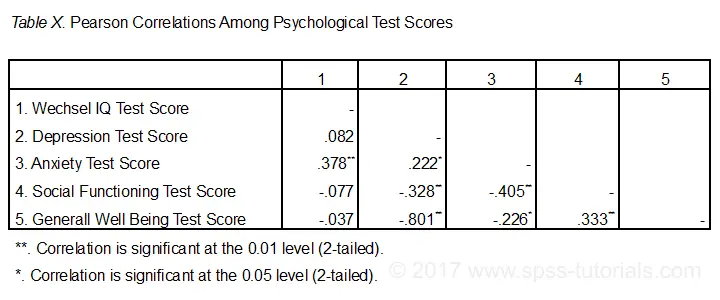
Melden Sie nach Möglichkeit auch die Konfidenzintervalle für Ihre Korrelationen., Seltsamerweise enthält SPSS diese nicht. Siehe jedoch SPSS Konfidenzintervalle für Korrelationen Werkzeug.

Danke fürs Lesen!